Visual C++で任意4点を持つ塗り潰し四角形を描画する方法

　作業環境：Windows2000, ++ 6.0, MFC AppWizard, MDI（or SDI）アプリケーション
　作成プロジェクト名：CQuadrilateral

　これらのプログラムは私が作成して使用しているプログラムですが、実際にお客様方がこれらをコンパイルや実行した際に何らかの悪影響が生じたとしても、管理人・九本麻有巣は一切の責任を負いかねます。御利用は、各人の責任を以ってお願い致します。

　MFC VC++ではデフォルトで幾つかの描画関数が用意されています。例えばラインを引く為の MoveTo, LineTo関数。円・楕円を描く為の Ellipse関数。矩形描画の為の FillRect関数。点描画用のSetPixel関数。これだけあれば簡単な配置地図とか程度なら描画できます。
　しかし、実際にVC++を用いていざ物を描こうと思った時、一つの致命的な欠陥に気付かれると思います。そう、「矩形は描けても、台形・平行四辺形を初めとする任意の4点から成る塗り潰し四角形を描画出来ない！！」。冷静に考えれば、わざわざVC++でイラスト描こうと言う方もいないと思うんであまり問題無いような気もしますが……。私はちょっとした事情でそれが必要となった。
　しかし、MFCではそれは用意されていない。では、どうしたか？答えは簡単。自分で作った。
　そんなワケで、その時作成した塗り潰し四角形描画関数をここで紹介したいと思います。

　さて、今からその説明なのですが、はっきり言って説明などは聞かなくっても利用は出来ます。ですから、「どう言うアルゴリズムで作った関数かなんて興味無い」と言う方は、下のコードを.cppファイル、.hファイルの適当な場所へそのままCopy & Pasteして使って下さい。

　まず、以下のコードを QuadrilateralView.h ファイル内のCQuadrilateralViewクラス内で宣言します。


class CQuadrilateral : public CView
{
        :
        :
public:
  void   FillQuadrilateral(CPoint pt1, CPoint pt2, CPoint pt3, CPoint pt4,  COLORREF crColor, CDC* pDC);   // メインとなる4点四角描画関数。
  double LineFunction(double lfAx, double lfAy, double lfBx, double lfBy, double lfX);     // FillQuadrilateral内で用いられる補助関数
        :
        :
};

　続いて以下のコードを QuadrilateralView.cpp ファイルに追加します。


void CQuadrilateral::FillQuadrilateral(CPoint pt1, CPoint pt2, CPoint pt3, CPoint pt4,  COLORREF crColor, CDC* pDC)
{
  // ■■ DECLEAR
  int        i,j;
  int        n;
  double     lfX[4], lfY[4];
  double     lfTempX, lfTempY;
  double     y1, y2;
  CPen       penNew;
  CPen*      ppenOld;

  // ■■ FORMAT
  lfX[0] = pt1.x;  lfX[1] = pt2.x;  lfX[2] = pt3.x;  lfX[3] = pt4.x;
  lfY[0] = pt1.y;  lfY[1] = pt2.y;  lfY[2] = pt3.y;  lfY[3] = pt4.y;
  penNew.CreatePen(PS_SOLID, 1, crColor);
  ppenOld = pDC->SelectObject(&penNew);

  // ■■ SUBSTANCE
  // [][] Bubble sort.
  for (j=0; j<3; j++)
  {
    for (i=0; i<3-j; i++)
    {
      if (lfX[i] >= lfX[i+1])
      {
        lfTempX = lfX[i];  lfX[i] = lfX[i+1];  lfX[i+1] = lfTempX;
        lfTempY = lfY[i];  lfY[i] = lfY[i+1];  lfY[i+1] = lfTempY;
      }
    }
  }

  y1 = LineFunction(lfX[0], lfY[0], lfX[3], lfY[3], lfX[1]);
  y2 = LineFunction(lfX[0], lfY[0], lfX[3], lfY[3], lfX[2]);

  if ( ((y1 <= lfY[1]) && (y2 <= lfY[2])) || ((y1 >= lfY[1]) && (y2 >= lfY[2])) )
    n = 1;
  else 
    n = 0;

  // [][] Fill quadrilateral area with desired color.
  for (i=(int)(lfX[0]); i<=lfX[1]; i++)
  {
    y1 = LineFunction(lfX[0], lfY[0], lfX[ 1 ], lfY[ 1 ], i);
    y2 = LineFunction(lfX[0], lfY[0], lfX[2+n], lfY[2+n], i);
    pDC->MoveTo(i,(int)(y1));
    pDC->LineTo(i,(int)(y2));
  }

  for (i=(int)(lfX[1]); i<=lfX[2]; i++)
  {
    y1 = LineFunction(lfX[0], lfY[0], lfX[2+n], lfY[2+n], i);
    y2 = LineFunction(lfX[1], lfY[1], lfX[3-n], lfY[3-n], i);
    pDC->MoveTo(i,(int)(y1));
    pDC->LineTo(i,(int)(y2));
  }

  for (i=(int)(lfX[2]); i<=lfX[3]; i++)
  {
    y1 = LineFunction(lfX[1-n], lfY[1-n], lfX[3], lfY[3], i);
    y2 = LineFunction(lfX[ 2 ], lfY[ 2 ], lfX[3], lfY[3], i);
    pDC->MoveTo(i,(int)(y1));
    pDC->LineTo(i,(int)(y2));
  }

  // [][] Settlement.
  pDC->SelectObject(ppenOld);
  penNew.DeleteObject();

  return;
}

double CQuadrilateral::LineFunction(double lfAx, double lfAy, double lfBx, double lfBy, double lfX)
{
  if ((lfAx-lfBx) == 0)
  {
    if (lfAy > lfBy)    { return lfAy; }
    else                { return lfBy; }
  }
	
  return ((lfAy-lfBy) / (lfAx-lfBx) * (lfX-lfAx) + lfAy);
}

　以上で終了です。あとは各Viewクラスで
　　Quadrilateral(CPoint pt1, CPoint pt2, CPoint pt3, CPoint pt4, COLORREF crColor, CDC *pDC);
　としてやるだけで、画面上に任意の4点を持つ四角領域を描画できます。
　引き数の意味については使い方は以下を参考にして下さい。


Quadrilateral(
    CPoint pt1,       // 1つ目の任意点
    CPoint pt2,       // 2つ目の任意点
    CPoint pt3,       // 3つ目の任意点
    CPoint pt4,       // 4つ目の任意点
    COLORREF crColor, // 四角形の中身を塗る色をRGBで指定
    CDC* pDC)         // デバイスコンテキストへのポインタ。解からなければそのままpDCを指定。

　では、唯今からこの関数のアルゴリズムについて説明したいと思います。興味がある方だけ、以下の説明に目を通して下さい。

関数のアルゴリズム
　1. DECLEAR
　ここは単なる型宣言ですので端折ります。
　2. FORMAT
　ここで、宣言した変数などの初期値を代入しています。
　lfX[0]〜lfX[3]及びlfY[0]〜lfY[3]に、引数として与えられた4点の値を代入しています。わざわざ配列型変数に代入するのは、その後の取り扱いを容易にする為です。以後、解説内では pt[i]=(lfX[i], lfY[i]) [i=0, 1, 2, 3]として表現します。
　続いて引数として与えられたRGB値を持つ実線ペンNewPenを作成して、そのペンを使用出来るように選択します。
　3. SUBSTANCE
　　3-1. Bubble sort.
　まず関数の先頭にある二重forループ。ここでは四角形の4点をX軸の負方向から順番になるように並び替えを行なっています。
　その下で行なっている計算は、また後程説明しますので、ここでは気にせずに、n=1として考えておいて下さい。
　　3-2. Fill quadrilateral area with desired color.
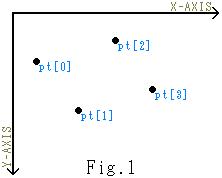Figure 1 　ここで4点四角の色塗りを行なっています。
　右のFig.1を見て下さい。4点はBubble sort部分で並び替えられたのでX軸の負方向から正方向へ順序良く並んでいます。今、この四角形を塗り潰したいのですが、どうすれば良いでしょうか？やり方は簡単。四角形内部を直線で埋めてやれば良いだけです。このFill quadrilateral部分では、それを実行しています。
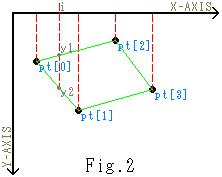Figure 2 　どう言う論拠でこれを直線で埋めているかと言うと――はい、Fig.2を見て下さい。
　まず、lfX[0]からlfX[1]まで、変数iを1[pixel]ずつ移動させてサーチを掛けます。そして各i毎に上辺(y1)から下辺(y2)に掛けて直線を引く（このy1、y2の値は、LineFunction関数で行なっています）。それをlfX[1]からlfX[2]、lfX[2]からlfX[3]、つまりlfX[0]からlfX[3]に掛けて行なえば、内部を指定カラーで塗り潰した4点四角形の完成、と言うわけです。
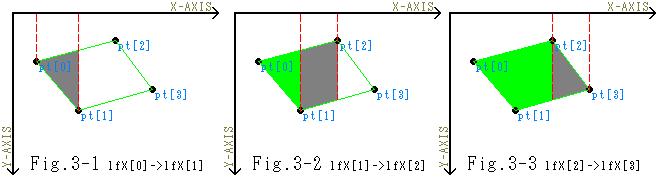Figure 3 　それをヴィジュアル的に見せますと、右図Fig.3のようになります。各X間隔毎に灰色の部分が順次塗り潰されていくわけです。
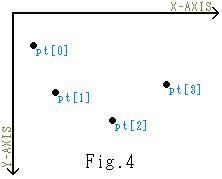Figure 4 　しかし、これには一つ重大な欠点があります。先刻までの例では、上辺下辺に対応する直線はX軸の値に対して、
　　lfX[0]-lfX[1] : 直線pt[0]pt[1]、直線pt[0]pt[2]
　　lfX[1]-lfX[2] : 直線pt[0]pt[2]、直線pt[1]pt[3]
　　lfX[2]-lfX[3] : 直線pt[1]pt[3]、直線pt[2]pt[3]
となっています。では、例えば左図Fig.4を見て下さい。
　もしも与えられた4点がFig.4のようだったらどうなるでしょう？次から次へと図が遷り変わって申し訳ないのですが、Fig.5を見て下さい。
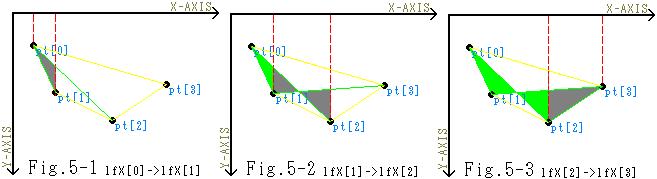Figure 5 　見てもらえれば一目瞭然でしょうが、本来黄色の枠内を塗って欲しいのに、見事に塗ってくれません。実際に四角形に塗り潰そうと思えば、対応する直線を
　　lfX[0]-lfX[1] : 直線pt[0]pt[3]、直線pt[0]pt[1]
　　lfX[1]-lfX[2] : 直線pt[0]pt[3]、直線pt[1]pt[2]
　　lfX[2]-lfX[3] : 直線pt[0]pt[3]、直線pt[2]pt[3]
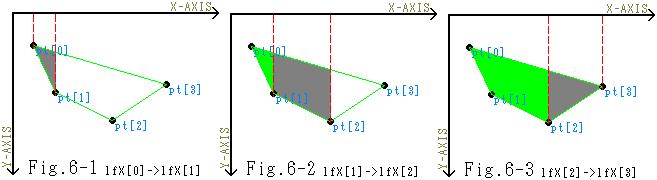Figure 6 　に変更する事を余儀なくされます。そうすれば、右図Fig.6のように無事に塗り潰しが完了します。
　ここで少し見て欲しいのですが、Fig.1〜3（以下：TypeA）とFig.4〜6（以下：TypeB）での直線式の対応に関して、下の表に纏めてみました。見てみて下さい。

　　　X軸の区間　　　　　 TypeAが使用する二直線　　　　　　　　TypeBが使用する二直線
　　lfX[0]-lfX[1]　:　直線pt[0]pt[1]、直線pt[0]pt[2]　　　直線pt[0]pt[3]、直線pt[0]pt[1]
　　lfX[1]-lfX[2]　:　直線pt[0]pt[2]、直線pt[1]pt[3]　　　直線pt[0]pt[3]、直線pt[1]pt[2]
　　lfX[2]-lfX[3]　:　直線pt[1]pt[3]、直線pt[2]pt[3]　　　直線pt[0]pt[3]、直線pt[2]pt[3]

　これを一つにまとめると、TypeAの時n=0、TypeBの時n=1として、

　　　X軸の区間　　　　　　　　　　使用する二直線
　　lfX[0]-lfX[1]　:　直線pt[ 0 ]pt[ 1 ]、直線pt[ 0 ]pt[2+n]
　　lfX[1]-lfX[2]　:　直線pt[ 0 ]pt[2+n]、直線pt[ 1 ]pt[3-n]
　　lfX[2]-lfX[3]　:　直線pt[1-n]pt[ 3 ]、直線pt[ 2 ]pt[ 3 ]

　として表わす事が出来ます。この"n"の値が、Bubble sortの一番下で設定されている値です。
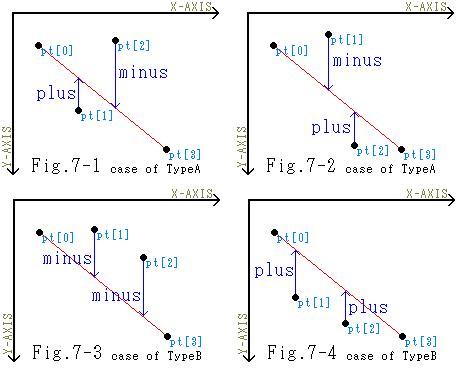Figure 7 　では、そのnの値を決定する決め手となる条件は何でしょうか？これに関しましてはFig.7を見て下さい。
　見てもらえば解かるかも知れませんが、TypeA（Fig.7-1 and 7-2）は、pt[1]とpt[2]が、直線pt[0]pt[3]の上側と下側に別れているケースであり、TypeB（Fig.7-3 and 7-4）は、pt[1]とpt[2]が、直線pt[0]pt[3]の上側と下側に固まっているケースである事が解かると思います。
　従って、それを判別さえすれば、nの値を決定する事が出来ます。それが、Bubble sort内でy1、y2を決定している箇所です。
　　3-3. Settlement.
　で、選択したペンをデフォルトのペン（ppenOld）に持ち替えて、描画に使用したペンをDeleteObject()関数で削除してメモリを開放して終了です。

　最後に、LineFunctionに関しましては、中学校の数学で習う二点を結ぶ直線の方程式上の点の求め方をそのまま利用しただけですので、こちらの方は教科書を紐解いて独自に理解して下さい。

　っとまァ、大したプログラムでは無かったですが、以上です。

Visual C++ プログラミング講座

Return to Top-page　　　 Return to Extra-Index